

Next: Markov-Chain Model for Reliability
Up: Reliability and Availability Analysis
Previous: Reliability and Availability Analysis
According to the given assumptions, we know that write requests
arrive in the duplication queue with an arrival rate of
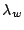 and leave the queue with a duplication rate of
and leave the queue with a duplication rate of
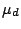 . For the system to be stable, it is implied that
. For the system to be stable, it is implied that
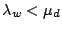 , otherwise the length of the duplication queue
will grow to infinity, causing the system to saturate. If the
number of requests in the queue is zero, we say that the data in
the primary node is consistent with the backup node. This
duplication queue can be modeled by an
, otherwise the length of the duplication queue
will grow to infinity, causing the system to saturate. If the
number of requests in the queue is zero, we say that the data in
the primary node is consistent with the backup node. This
duplication queue can be modeled by an 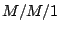 queuing
model [31][32].
In the model, the probability of the consistent
state, i.e., the probability of an empty queue, can be calculated as follows:
queuing
model [31][32].
In the model, the probability of the consistent
state, i.e., the probability of an empty queue, can be calculated as follows:
Although 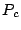 is derived based on the duplication process of
Protocol 1, this term can also be used in other protocols. In
Protocol 2 and 4, all data has already been duplicated to the
mirror nodes at the time when the client nodes complete the
writing access. Thus
is derived based on the duplication process of
Protocol 1, this term can also be used in other protocols. In
Protocol 2 and 4, all data has already been duplicated to the
mirror nodes at the time when the client nodes complete the
writing access. Thus 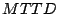 can be thought to be 0. In Protocol 3,
at the time the client finishes the writing process, there is
still a chance that a primary node is not consistent with the its
backup node. Similarly, it can also be modeled as
can be thought to be 0. In Protocol 3,
at the time the client finishes the writing process, there is
still a chance that a primary node is not consistent with the its
backup node. Similarly, it can also be modeled as 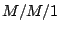 theoretically if we redefine
theoretically if we redefine 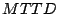 as the difference between the
time instants when data is stored in the faster server and when
data is stored in the slower server node.
as the difference between the
time instants when data is stored in the faster server and when
data is stored in the slower server node.


Next: Markov-Chain Model for Reliability
Up: Reliability and Availability Analysis
Previous: Reliability and Availability Analysis
Yifeng Zhu
2003-10-16
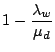

![]() is derived based on the duplication process of
Protocol 1, this term can also be used in other protocols. In
Protocol 2 and 4, all data has already been duplicated to the
mirror nodes at the time when the client nodes complete the
writing access. Thus
is derived based on the duplication process of
Protocol 1, this term can also be used in other protocols. In
Protocol 2 and 4, all data has already been duplicated to the
mirror nodes at the time when the client nodes complete the
writing access. Thus ![]() can be thought to be 0. In Protocol 3,
at the time the client finishes the writing process, there is
still a chance that a primary node is not consistent with the its
backup node. Similarly, it can also be modeled as
can be thought to be 0. In Protocol 3,
at the time the client finishes the writing process, there is
still a chance that a primary node is not consistent with the its
backup node. Similarly, it can also be modeled as ![]() theoretically if we redefine
theoretically if we redefine ![]() as the difference between the
time instants when data is stored in the faster server and when
data is stored in the slower server node.
as the difference between the
time instants when data is stored in the faster server and when
data is stored in the slower server node.